See It, Say It, Symbolize It

Transformation of Functions

See it

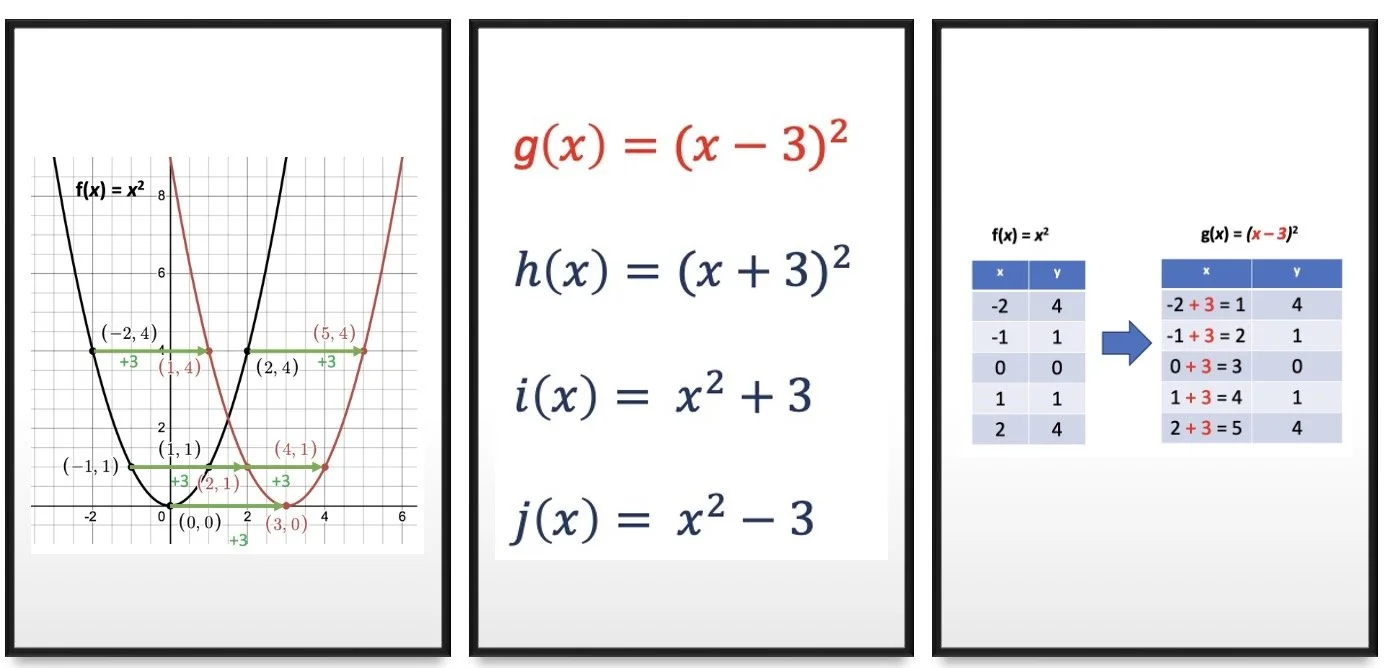
Graph of f(x).

Let's examine this idea through an example of transformations of functions. In this particular instance what we want to make explicit is what happens to the input and output values of a parent function after a transformation. To see this a graphical representation with particular ordered pairs illuminated seems most appropriate. We want students to “see” that the input values of f(x) changed, but the output values remained the same.

Say it

When asked about the transformation of f(x) to create the graph shown in red students commonly respond with the phrase “it shifted three units to the right”. While the statement is true the language is not conceptually consistent. Since a function describes a relationship between input and output values it is important to press students to communicate what happens to both the input and output values. In this instance the corresponding input values increased by 3 while the corresponding output values remained the same.

Symbolize it

When writing the symbolic description of the transformation students often provide one of the four choices in the image above and memorize without knowing “why”. Leveraging the “Say it” we can emphasize that since the change happened on the input values of the parent function f(x) this change must occur symbolically before the squaring operation of the function—thus it must be inside the parentheses [ruling out i(x) and j(x)] AND it must be done while keeping the output values the same. The only choice of a function rule that aligns with the graphical representation is g(x). This can be also be seen in the table of values shown above.

In the future as students “look through” a function rule, such as j(x), they will have a mental image of graph to see that transformation is a vertical shift of 3 units downward while communicating that this means that the corresponding input values remained the same while each of the corresponding output values decreased by 3.